RU |
||||||||
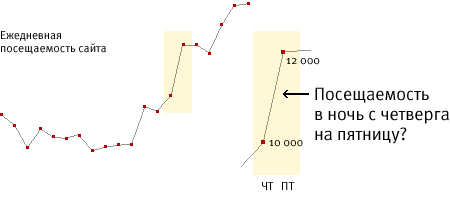
| Один из самых распространенных приемов визуализации ряда числовых данных — псевдокривая (гр. pseudos, ложь), грубо соединяющая точки, соответствующие данным этого ряда. Проблема в том, что достоверными являются только основные точки псевдокривой, а промежуточные точки либо не соответствуют действительности, либо бессмысленны. Псевдокривая может легко ввести зрителя в заблуждение. | ||||||||
 |
| Чаще всего этот прием некорректно используется в интервальных хронологических рядах, таких как объем продаж, посещаемость сайта, среднесуточная температура. В интервальных рядах каждое измеренное значение по оси Y соответствует определенному интервалу, а не точке, на оси X. Посещаемость сайта измеряется не в определенное мгновение, а за промежуток времени — день, месяц, год. Выбранному периоду соответствует постоянная величина, которая не растет и не падает. | ||||||||
| Интервальные данные в статистике принято изображать гистограммами (гр. histos, столб) — столбиковыми диаграммами. Теоретически в гистограммах ширина интервалов, которым соответствуют данные, может быть неодинакова. В общем случае гистограмма изображается в виде прямоугольников с неравной шириной, площадь (а не высота!) которых пропорциональна изображаемым данным. | Гистограмма в БСЭ | |||||||
|
| На практике гистограммы с неравными основаниями неудобны для восприятия, поэтому интервалы обычно выбираются одинаковые. При равной ширине площадь прямоугольников прямо пропорциональна их высоте, поэтому в обычной гистограмме сравнивается только высота столбиков. Это дает возможность улучшить дизайн традиционных гистограмм. | ||||||||
| ||||||
|
Во всех вариантах явно различается каждое вычисленное (или полученное экспериментально) значение —
тогда как неэтичная псевдокривая скрывает от нас факты: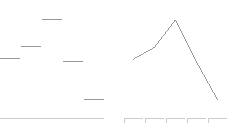 |
||||||||
| Иногда в защиту псевдокривой приводится аргумент, что угол ее наклона легко определить на глаз, что позволяет более тонко оценить скорость прироста, чем по «ступенькам» гистограммы. Однако визуальная грубость гистограммы является следствием ее природы: чаще всего она отображает агрегаты (среднее арифметическое, сумма) на широких интервалах. Она показывает упрощенные данные о реальности и не скрывает этого. | ||||||||
| Заметим, что с уменьшением ширины интервалов (и увеличением количества представляемых данных) гистограмма постепенно превращается в плавный график, позволяющий анализировать тонкие изменения на реальных данных. | ||||||||
| В экспериментальной статистике ученый имеет дело с конечным эмпирическим рядом данных. Для поиска закономерности, лежащей в основе экспериментальных данных, применяется выравнивание (в англоязычной литературе fitting). | Выравнивание в БСЭ | |||||||
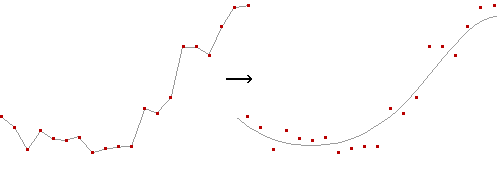 |
| Различные методики выравнивания позволяют построить плавную «выравнивающую» кривую. Правильно подобранная кривая наглядно выявляет теоретическую закономерность и фактор случайности, вызвавший разброс фактических значений. | ||||||||
| В то же время скачкообразное изменение наклона псевдокривой отражает только случайные колебания и скрывает общую картину. | ||||||||
| Все сказанное здесь о псевдокривых не означает, что ими нельзя пользоваться. Например, может стоять задача отобразить на одной диаграмме результаты десятков экспериментов, в каждом из которых был получен свой ряд данных (набор точек). Если отобразить все данные в виде отдельных точек, получится беспорядочное облако, т. к. каждый эксперимент проводился в своих уникальных условиях. Но если соединить точки каждого отдельного эксперимента тонкими линиями, то на диаграмме можно будет отличить данные одного эксперимента от другого. В данном случае линии будут играть роль идентификатора, а не бесполезной обводки. | ||||||||